Customizations
In this page we'll dive deeper into several aspects of our React Native iOS module that can be customized to match your needs.
Library Options
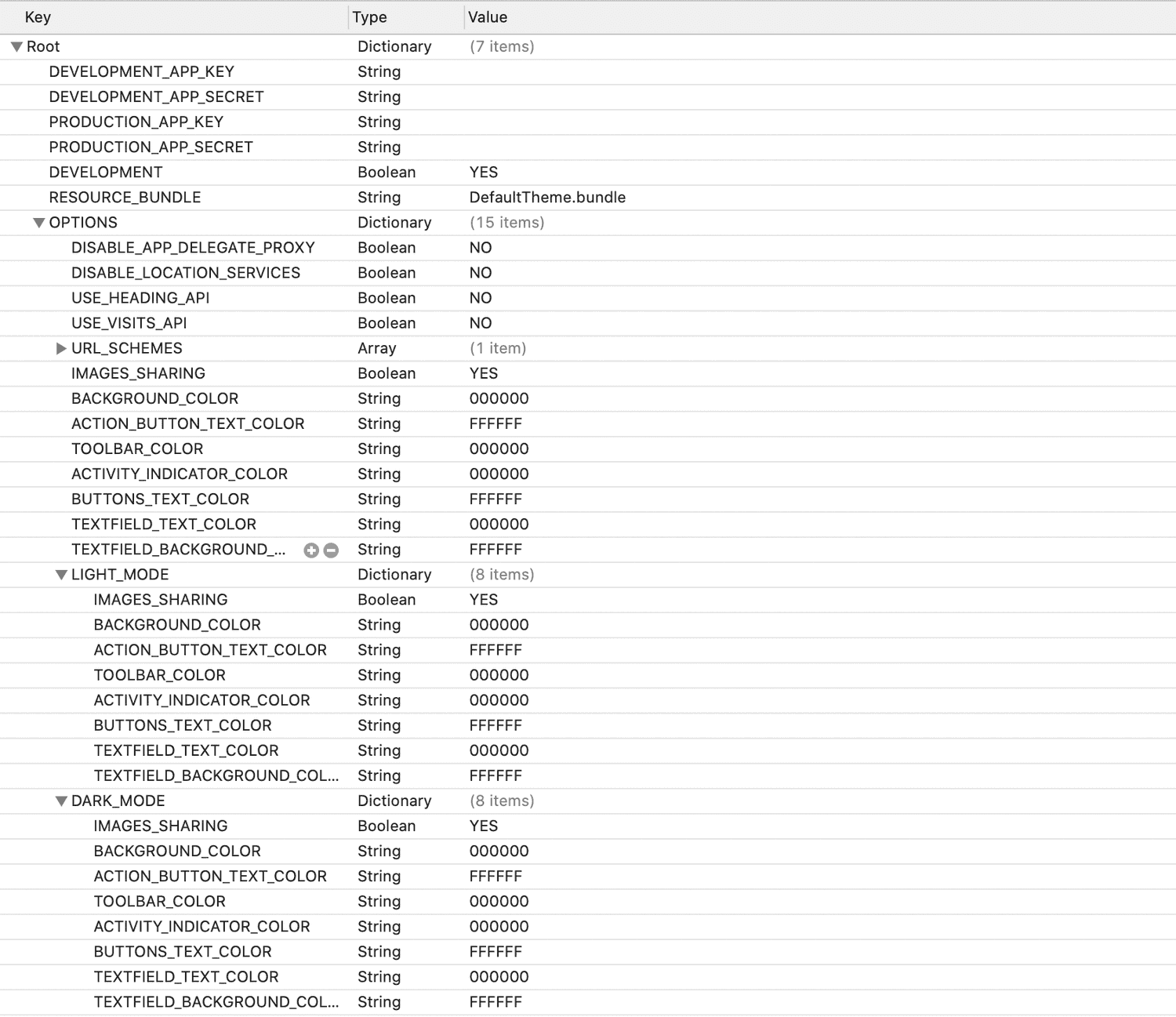
The Notificare.plist is used by the library for setup and customization. It allows you to change the colours of the notifications' user interface or enable/disable certain functionality. By default we provide a colour scheme for some of our UI elements that might not match your app's look and feel and using the options below, you will be able to change that look & feel. Open you Notificare.plist and change the following properties if needed.
Localizable Texts
Our library ships with a default theme that can be customized if needed. Inside the DefaultTheme.bundle you will find several localized folders that contain all the texts used in the library. You are free to change those texts to match your needs and even add new languages if needed.

Using a Strings Dictionary for Rich Push Templates
In iOS 11, Apple extended hidden previews texts to all the apps. This will allow you to display a pre-defined text whenever a user chooses to hide the content of a notification preview in the lock screen or notification center. Include a Localizable.stringsdict file in your project, like the one below, in order to handle those texts correctly:

Please note that Notificare will have a default category for you that will apply to all your notifications so you must provide a text for the NotificareDefaultCategory and if you are using Rich Push Templates you should also create an entry for each template in your app.
In your Localizable.stringsdict file you should add the following entry for the default category and eventually several other entries that match your Rich Push Templates:
<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE plist PUBLIC "-//Apple//DTD PLIST 1.0//EN" "http://www.apple.com/DTDs/PropertyList-1.0.dtd">
<plist version="1.0">
<dict>
<key>NotificareDefaultCategory</key>
<dict>
<key>NSStringLocalizedFormatKey</key>
<string>%#@notification@</string>
<key>notification</key>
<dict>
<key>NSStringFormatSpecTypeKey</key>
<string>NSStringPluralRuleType</string>
<key>NSStringFormatValueTypeKey</key>
<string>u</string>
<key>zero</key>
<string></string>
<key>one</key>
<string>%u notification</string>
<key>two</key>
<string></string>
<key>few</key>
<string></string>
<key>many</key>
<string></string>
<key>other</key>
<string>%u notifications</string>
</dict>
</dict>
<key>MY_RICH_PUSH_TEMPLATE_TITLE</key>
<dict>
<key>NSStringLocalizedFormatKey</key>
<string>%#@question@</string>
<key>question</key>
<dict>
<key>NSStringFormatSpecTypeKey</key>
<string>NSStringPluralRuleType</string>
<key>NSStringFormatValueTypeKey</key>
<string>u</string>
<key>zero</key>
<string></string>
<key>one</key>
<string>%u message awaits your answer</string>
<key>two</key>
<string></string>
<key>few</key>
<string></string>
<key>many</key>
<string></string>
<key>other</key>
<string>%u messages awaits your answer</string>
</dict>
</dict>
</dict>
</plist>If your app supports several languages, repeat the operation for every localization file. This will allow you to customize how your notifications show in the lock screen when Hidden Previews are enabled: